这道毒瘤到极致的最大流真的不是欣姐出的

在学习最大流之前，让我们先认识一下流网络：

G=（V，E）是一个有向图，其中每条边（u，v）有一个非负的容量值c（u，v），而且如果E中包含一条边（u，v），那么图中就不存在它的反向边。在流网络中有两个特殊的结点，源结点s和汇点t。

下面给出流网络的形式化定义。令G=（V，E）为一个流网络，其容量函数为c，设s我为网络的源点，t为汇点。G中的流是一个实值函数f，满足以下两条性质：

1. 容量限制（capacity contraint）：对于所有的结点u，v，要求

2. 流量守恒（flow conservation）：对于所有的非源点和汇点的结点u，要求：

下图是一个流网络的示例图，帮助大家理解，其中的“/”只是分隔符而不是运算符，“/”前代表的是流的值，后面的数值则是该条边的容量（capacity）：

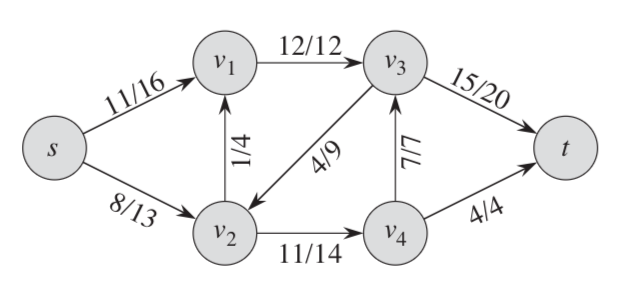
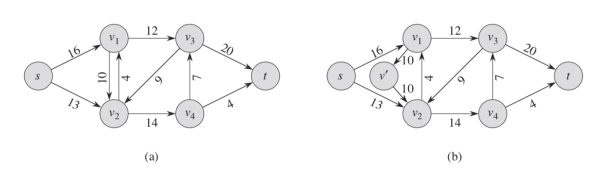
流网络常见的一种应用场景是运输问题，需要将货物从s运输到t，途经几个中转站，每次运输到每个中转站的货物的数量是有限制的。在实际应用中我们可能会在某条边上双向运输，这样便违反了我们之前对流网络的定义，但是我们可以将包含反平行边的图来改造成流网络，具体的方法是引入一个是虚构的中转结点，方法如下图。

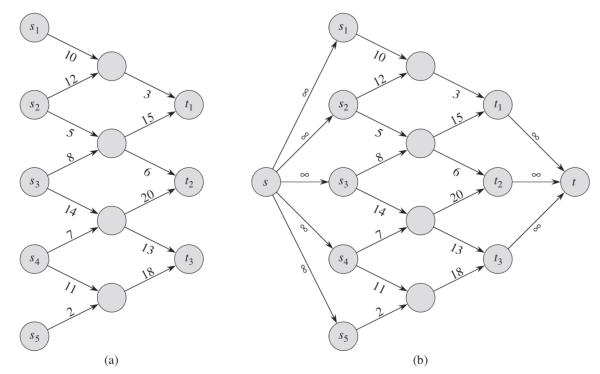
考虑另外一种特殊情形，从多个工厂发出货物最终运输到别的多个工厂，这时候我们具有了多个源点和多个汇点，这也很好解决，解决的方法就是人为添加超级源点（supersource）和超级汇点（supersink），具体方法见下图。

现在给你n+2个节点，其中1~n号节点按照有向边i指向i+1连城一个环（注意，n号节点连向1号节点）

每条有向边有一个限流值，记为vi，0号节点作为源点，即该点初始的流量是无限的，n+1号节点作为汇点，即最后流量到达的点。

你可以任意选择一个点x（1<=x<=n），让0号节点指向x号节点，然后上一节点指向n+1号节点，XrkArul想知道选择最优节点时，流入最大汇点的流量是多少。

第一行一个整数n（1<=n<=100000），代表点的个数。

第二行n个整数vi表示i到i+1的有向边可以通过的最大流量，vn表示n号节点连向1号节点，数据保证vi为正整数且在int范围内。

输出一个整数表示该图的最大流

4
1 1 1 1

1