Random Events

Ron is a happy owner of a permutation a of length n.

A permutation of length n is an array consisting of n distinct integers from 1 to n in arbitrary order. For example, [2,3,1,5,4] is a permutation, but [1,2,2] is not a permutation (2 appears twice in the array) and [1,3,4] is also not a permutation (n=3 but there is 4 in the array).

Ron's permutation is subjected to m experiments of the following type: (r_i, p_i). This means that elements in range [1, r_i] (in other words, the prefix of length r_i) have to be sorted in ascending order with the probability of p_i. All experiments are performed in the same order in which they are specified in the input data.

As an example, let's take a look at a permutation [4, 2, 1, 5, 3] and an experiment (3, 0.6). After such an experiment with the probability of 60% the permutation will assume the form [1, 2, 4, 5, 3] and with a 40% probability it will remain unchanged.

You have to determine the probability of the permutation becoming completely sorted in ascending order after m experiments.

Each test contains one or more test cases. The first line contains the number of test cases t (1 ≤ t ≤ 100).

The first line of each test case contains two integers n and m (1 ≤ n, m ≤ 10^5) — the length of the permutation and the number of experiments, respectively.

The second line of each test case contains n integers a_1, a_2, ……, a_n (1 ≤ a_i ≤ n) — contents of the permutation.

The following m lines of each test case each contain an integer r_i and a real number p_i (1 ≤ r_i ≤ n, 0 ≤ p_i ≤ 1) — the length of the prefix and the probability of it being sorted. All probabilities are given with at most 6 decimal places.

It is guaranteed that the sum of n and the sum of m does not exceed 10^5 ().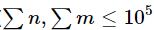

For each test case, print a single number — the probability that after all experiments the permutation becomes sorted in ascending order. Your answer will be considered correct if its absolute or relative error does not exceed 10^{-6}.

Formally, let your answer be a, and the jury's answer be b. Your answer is accepted if and only if .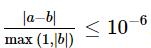

4
4 3
4 3 2 1
1 0.3
3 1
4 0.6
5 3
4 2 1 3 5
3 0.8
4 0.6
5 0.3
6 5
1 3 2 4 5 6
4 0.9
5 0.3
2 0.4
6 0.7
3 0.5
4 2
1 2 3 4
2 0.5
4 0.1

0.600000
0.720000
0.989500
1.000000

 Note

Explanation of the first test case: It can be demonstrated that whether the final permutation is sorted or not depends solely on sorting being performed in the (4, 0.6) experiment.