Find the Spruce

Holidays are coming up really soon. Rick realized that it's time to think about buying a traditional spruce tree. But Rick doesn't want real trees to get hurt so he decided to find some in an n * m matrix consisting of "*" and ".".

To find every spruce first let's define what a spruce in the matrix is. A set of matrix cells is called a spruce of height k with origin at point (x, y) if:

• All cells in the set contain an "*".

• For each 1 ≤ i ≤ k all cells with the row number x+i-1 and columns in range [y - i + 1, y + i - 1] must be a part of the set. All other cells cannot belong to the set.

Examples of correct and incorrect spruce trees:

Now Rick wants to know how many spruces his n * m matrix contains. Help Rick solve this problem.

Each test contains one or more test cases. The first line contains the number of test cases t (1 ≤ t ≤ 10).

The first line of each test case contains two integers n and m (1 ≤ n, m ≤ 500) — matrix size.

Next n lines of each test case contain m characters c_{i, j} — matrix contents. It is guaranteed that c_{i, j} is either a "." or an "*".

It is guaranteed that the sum of n * m over all test cases does not exceed .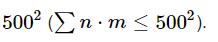

For each test case, print single integer — the total number of spruces in the matrix.

4
2 3
.*.
***
2 3
.*.
**.
4 5
.***.
*****
*****
*.*.*
5 7
..*.*..
.*****.
*******
.*****.
..*.*..

5
3
23
34

 Note

In the first test case the first spruce of height 2 has its origin at point (1, 2), the second spruce of height 1 has its origin at point (1, 2), the third spruce of height 1 has its origin at point (2, 1), the fourth spruce of height 1 has its origin at point (2, 2), the fifth spruce of height 1 has its origin at point (2, 3).
In the second test case the first spruce of height 1 has its origin at point (1, 2), the second spruce of height 1 has its origin at point (2, 1), the third spruce of height 1 has its origin at point (2, 2).