Minimum Grid Path
Let's say you are standing on the XY-plane at point (0, 0) and you want to reach point (n, n).
You can move only in two directions:
to the right, i. e. horizontally and in the direction that increase your x coordinate,
or up, i. e. vertically and in the direction that increase your y coordinate.
In other words, your path will have the following structure:
initially, you choose to go to the right or up;
then you go some positive integer distance in the chosen direction (distances can be chosen independently);
after that you change your direction (from right to up, or from up to right) and repeat the process.
You don't like to change your direction too much, so you will make no more than n - 1 direction changes.
As a result, your path will be a polygonal chain from (0, 0) to (n, n), consisting of at most n line segments where each segment has positive integer length and vertical and horizontal segments alternate.
Not all paths are equal. You have n integers c_1, c_2, ……, c_n where c_i is the cost of the i-th segment.
Using these costs we can define the cost of the path as the sum of lengths of the segments of this path multiplied by their cost, i. e. if the path consists of k segments (k ≤ n), then the cost of the path is equal to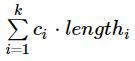 
(segments are numbered from 1 to k in the order they are in the path).
Find the path of the minimum cost and print its cost.
The first line contains the single integer t (1 ≤ t ≤ 1000) — the number of test cases.
The first line of each test case contains the single integer n (2 ≤ n ≤ 10^5).
The second line of each test case contains n integers c_1, c_2, ……, c_n (1 ≤ c_i ≤ 10^9) — the costs of each segment.
It's guaranteed that the total sum of n doesn't exceed 10^5.
For each test case, print the minimum possible cost of the path from (0, 0) to (n, n) consisting of at most n alternating segments.
3 2 13 88 3 2 3 1 5 4 3 2 1 4
202 13 19NoteIn the first test case, to reach (2, 2) you need to make at least one turn, so your path will consist of exactly 2 segments: one horizontal of length 2 and one vertical of length 2. The cost of the path will be equal to 2 * c_1 + 2 * c_2 = 26 + 176 = 202.
In the second test case, one of the optimal paths consists of 3 segments: the first segment of length 1, the second segment of length 3 and the third segment of length 2.
The cost of the path is 1 * 2 + 3 * 3 + 2 * 1 = 13.
In the third test case, one of the optimal paths consists of 4 segments: the first segment of length 1, the second one — 1, the third one — 4, the fourth one — 4. The cost of the path is 1 * 4 + 1 * 3 + 4 * 2 + 4 * 1 = 19.