Neko Performs Cat Furrier Transform

Cat Furrier Transform is a popular algorithm among cat programmers to create longcats. As one of the greatest cat programmers ever exist, Neko wants to utilize this algorithm to create the perfect longcat.

Assume that we have a cat with a number x. A perfect longcat is a cat with a number equal 2^m - 1 for some non-negative integer m. For example, the numbers 0, 1, 3, 7, 15 and so on are suitable for the perfect longcats.

In the Cat Furrier Transform, the following operations can be performed on x:

• (Operation A): you select any non-negative integer n and replace x with x ⊕ (2^n - 1), with ⊕ being a bitwise XOR operator.

• (Operation B): replace x with x + 1.

The first applied operation must be of type A, the second of type B, the third of type A again, and so on. Formally, if we number operations from one in the order they are executed, then odd-numbered operations must be of type A and the even-numbered operations must be of type B.

Neko wants to produce perfect longcats at industrial scale, thus for each cat Neko only wants to perform at most 40 operations. Can you help Neko writing a transformation plan?

Note that it is not required to minimize the number of operations. You just need to use no more than 40 operations.

The only line contains a single integer x (1 ≤ x ≤ 10^6).

The first line should contain a single integer t (0 ≤ t ≤ 40) — the number of operations to apply.

Then for each odd-numbered operation print the corresponding number n_i in it. That is, print 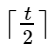integers n_i (0 ≤ n_i ≤ 30), denoting the replacement x with x ⊕ (2^{n_i} - 1) in the corresponding step.

If there are multiple possible answers, you can print any of them. It is possible to show, that there is at least one answer in the constraints of this problem.

39

4
5 3

1

0

7

0

 Note

In the first test, one of the transforms might be as follows: 39 → 56 → 57 → 62 → 63. Or more precisely:

 
 Pick n = 5. x is transformed into 39 ⊕ 31, or 56. 
 
 Increase x by 1, changing its value to 57. 
 
 Pick n = 3. x is transformed into 57 ⊕ 7, or 62. 
 
 Increase x by 1, changing its value to 63 = 2^6 - 1. 

In the second and third test, the number already satisfies the goal requirement.