Mr.Lin and gradient descent
In machine learning, there is a class of problems called unconstrained optimization problems, and gradient descent is one of the most commonly used methods. Given a simple convex function, please answer the minimum value of this convex function according to the gradient descent algorithm.
I guess you probably won't have a gradient descent algorithm, so we'll give you a gradient descent algorithm that you can implement.
The first step of the algorithm, based on the point (x1, x2, …, xn) on the curve, we need to determine the gradient of the loss function at the current position. For each
xi, the gradient expression is as follows:
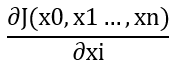
In the second step of the algorithm, the step size is multiplied by the gradient of the loss function to obtain the distance at which the current position falls, that is,
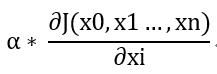
We can assume that α is any real number greater than 0 and less than 1, you can think α = 0.5.
In the third step of the algorithm, it is determined whether all θi, the distance of the gradient drop is less than ε, if all of them are less than ε, the algorithm terminates, and all current θi (i=0, 1, . . . n) is the final result. and current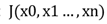
is the answer.
Otherwise go to step 4.
The fourth step of the algorithm updates all x. for xi, its update expression is as follows.
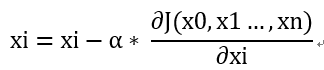
After the update is complete, proceed to step 1.
For make the problem more simply, all the convex functions we give are quadratic functions and the points on a quadratic function. Please find the minimum value of the given convex function with an error precision less than 1e-6.
上面都是废话，直接看这里
给你一个一元二次函数让你求最小值，保证a>0
There multiple test cases in the input
for each test case contain one line means a quadratic function, guarantee the function is a convex function, and a point in curve(-200< xi < 200), separated by space
all coefficient are real number greater than 0
For each test case output a real number means the minimum value of quadratic function.
y=x^2 (2,4) y=2*x^2+1 (3,19)
0.000000 1.000000