Sum of Factorials

John von Neumann, b. Dec. 28, 1903, d. Feb. 8, 1957, was a Hungarian-American mathematician who made important contributions to the foundations of mathematics, logic, quantum physics, meteorology, science, computers, and game theory. He was noted for a phenomenal memory and the speed with which he absorbed ideas and solved problems. In 1925 he received a B.S. diploma in chemical engineering from Zurich Institute and in 1926 a Ph.D. in mathematics from the University of Budapest. His Ph.D. dissertation on set theory was an important contribution to the subject. At the age of 20, von Neumann proposed a new definition of ordinal numbers that was universally adopted. While still in his twenties, he made many contributions in both pure and applied mathematics that established him as a mathematician of unusual depth. His Mathematical Foundations of Quantum Mechanics (1932) built a solid framework for the new scientific discipline. During this time he also proved the mini-max theorem of GAME THEORY. He gradually expanded his work in game theory, and with coauthor Oskar Morgenstern he wrote Theory of Games and Economic Behavior (1944).

There are some numbers which can be expressed by the sum of factorials. For example 9,9=1!+2!+3!. Dr. von Neumann was very interested in such numbers. So, he gives you a number n, and wants you to tell him whether or not the number can be expressed by the sum of some factorials.

Well, it's just a piece of cake. For a given n, you'll check if there are some xi, and let n equal to

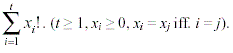
If the answer is yes, say "YES"; otherwise, print out "NO".

9
-1

YES