多项式插值(简单版)
TimeLimit:4000MS MemoryLimit:128MB
64-bit integer IO format:%lld
未提交 | 登录后收藏
Problem Description
首先我们先来个最简单的等距插值-打表神器(写起来一点也不简单 )
)
给一个n-1次多项p(x)=a0+a1x+a2x2+……+an-1xn-1 在 x=1,x=2,……x=n 处的取值。求a0,a1,a2……an-1的值 mod 1e9+7
注意an-1 可能 等于0
因为涉及到多项式乘法,这里提示一下。
对于(x+c1)(x+c2)……(x+cn)
这种乘法有个O(n2)背包算法(如果你会 NTT的话当我没说,你可以不用看):
先把每步乘法转化为
p(x)*(x-c)=x*p(x)+c*p(x) 的形式
所以每次只要把p(x)的系数数组移一位。再加上c倍原来的p(x)就行了
用代码表示就是
for(i=n-1;i>=0;i--)
{
a[i]=c*a[i];
if(i>0)
a[i]+=a[i-1];
a[i]%=mod;
}
Input
有多组数据
每次组据第一行,有一个整数n ,代表有n个点(1,2,3,……n)
接下来一行是这n个点的函数值(整数)p(1),p(2),p(3)……p(n)
0<n<=1e2
0<=p(i)<=1e4
数据的组数小于100
Output
对于每组数据输出n个整数,代表 a0,a1,……an-1的值。
因为数字可能会很大,或者出现分母。所以请将ai 模 1e9+7 后 输出。 若ai=p/q 请输出p*q-1 %(1e9+7)
其中q-1 为 q 在mod 1e9+7下的 乘法逆元 具体公式是 q-1 = p1e9+5%mod。
此时会有以下性质,方便大家验证自己的算法。
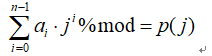
SampleInput
3 1 2 3 3 1 4 9 9 1 2 3 4 5 4 3 2 1
SampleOutput
0 1 0 0 0 1 70 261904580 692063688 805555458 743055593 972222223 63888890 960317467 500992067