CCL的地图

       CCL有一张地图，上面有很多点，那些点有各自的经纬度，CCL靠着这张地图上标记的点找到了一个又一个的宝藏过上了幸福的生活。有一天，CCL在1公顷的卧室里看着1KM远处的墙上的藏宝图，他思索起了这样一个问题，这张图上最近两点有多近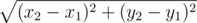，于是他就写了这样一个代码：

input n
for i from 1 to n
    input the i-th point's coordinates into p[i]
sort array p[] by increasing of x coordinate first and increasing of y coordinate second
d=INF        //here INF is a number big enough
tot=0
for i from 1 to n
    for j from (i+1) to n
        ++tot
        if (p[j].x-p[i].x>=d) then break    //notice that "break" is only to be
                                            //out of the loop "for j"
        d=min(d,distance(p[i],p[j]))
output d

CCL将tot作为代码的一个指标，然后给出了一个k当限制值，他想知道有没有一组坐标系数据可以让tot超过k，但是你懂的，故事里的主人公永远只会抛出问题，所以说，这题他又拿来问你了。

A single line which contains two space-separated integers n and k (2 ≤ n ≤ 2000, 1 ≤ k ≤ 10⁹).

输入只有一行，两个整数，n(n组坐标 ，2<=n<=2000)，k(限制值， 1<=k<=1e9)；

If there doesn't exist such a data which let the given code get TLE, print "no solution" (without quotes); else print n lines, and the i-th line contains two integers x_i, y_i (|x_i|, |y_i| ≤ 10⁹) representing the coordinates of the i-th point.

The conditions below must be held:

• All the points must be distinct.

• |x_i|, |y_i| ≤ 10⁹.

• After running the given code, the value of tot should be larger than k.

如果没有数据可以让tot超过k，输出“no solution”。

否则输出n组坐标数据（|xi|<=1e9, |yi|<1e9）

4 3

0 0
0 1
1 0
1 1

2 100

no solution