Subway Innovation

Berland is going through tough times — the dirt price has dropped and that is a blow to the country's economy. Everybody knows that Berland is the top world dirt exporter!

The President of Berland was forced to leave only k of the currently existing n subway stations.

The subway stations are located on a straight line one after another, the trains consecutively visit the stations as they move. You can assume that the stations are on the Ox axis, the i-th station is at point with coordinate x_i. In such case the distance between stations i and j is calculated by a simple formula |x_i - x_j|.

Currently, the Ministry of Transport is choosing which stations to close and which ones to leave. Obviously, the residents of the capital won't be too enthusiastic about the innovation, so it was decided to show the best side to the people. The Ministry of Transport wants to choose such k stations that minimize the average commute time in the subway!

Assuming that the train speed is constant (it is a fixed value), the average commute time in the subway is calculated as the sum of pairwise distances between stations, divided by the number of pairs (that is 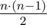) and divided by the speed of the train.

Help the Minister of Transport to solve this difficult problem. Write a program that, given the location of the stations selects such k stations that the average commute time in the subway is minimized.

The first line of the input contains integer n (3 ≤ n ≤ 3·10⁵) — the number of the stations before the innovation. The second line contains the coordinates of the stations x₁, x₂, ..., x_n ( - 10⁸ ≤ x_i ≤ 10⁸). The third line contains integer k (2 ≤ k ≤ n - 1) — the number of stations after the innovation.

The station coordinates are distinct and not necessarily sorted.

Print a sequence of k distinct integers t₁, t₂, ..., t_k (1 ≤ t_j ≤ n) — the numbers of the stations that should be left after the innovation in arbitrary order. Assume that the stations are numbered 1 through n in the order they are given in the input. The number of stations you print must have the minimum possible average commute time among all possible ways to choose k stations. If there are multiple such ways, you are allowed to print any of them.

3
1 100 101
2

2 3

 Note

In the sample testcase the optimal answer is to destroy the first station (with x = 1). The average commute time will be equal to 1 in this way.