Bridge

悬索桥凭借钢缆悬在空中，这些巨大的钢缆从桥的一头延伸到另一头。钢缆被固定在高塔上，两端用锚碇钉牢。这些塔使得钢缆能够延伸漫长的距离。

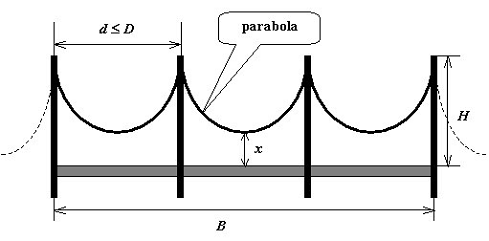
假设两座相邻塔间的最大距离是D，从塔顶到桥面的距离是H。同时假设所有两座相邻塔间的钢缆形状都是同样的对称抛物线（如图所示）。现在给出桥长B，钢缆总长，假设塔的数量尽可能少，要求你计算钢缆最低点到桥面的距离（假定桥的两端各建了一座塔）。

输入包含多组数据。

输入文件的第一行是一个正整数T(1<=T<=10)，代表数据组数。

下面是T组数据。

每组数据占一行，包含4个正整数：

D——两塔之间的最大距离

H——塔顶到桥面的距离

B——桥长

L——钢缆总长

数据保证B<=L，钢缆总是悬在路的上方。

对每组数据，先输出一行"Case #:"，其中#是数据组数，从1开始编号。

对每组数据，输出桥面到钢缆最低点的距离。保留两位小数。

2
20 101 400 4042
1 2 3 4 

Case 1:
1.00
Case 2:
1.60