矩阵与坐标变换

三大基础初等坐标变化包括

旋转变换:

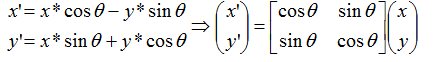
伸缩变换:

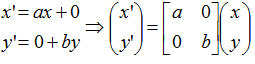
平移变换:

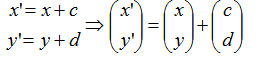
其他任意初等坐标变换的都可以由这三个变换经有限次复合得到。

所以任意初等变化都可以表示成以下形式

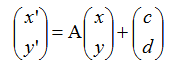
比如绕着（a,b）旋转θ可以看成，平移（-a,-b），旋转θ，平移（a,b）这三步复合得到，即

有多组数据

每组数据包含4个整数a,b,n,m

表示以（a,b）为中心，横坐标扩大n倍,纵坐标扩大m

求这个变换的标准形式

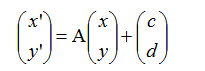
中的矩阵A,和向量(c,d)'

输出由3行整数组成，每行包含两个数字，数字之间用空格隔开

前两行代表A的系数

最后一行代表c和d

1 1 1 1
2 1 2 1

1 0
0 1
0 0
2 0
0 1
-2 0