Valera and Tubes

Valera has got a rectangle table consisting of n rows and m columns. Valera numbered the table rows starting from one, from top to bottom and the columns – starting from one, from left to right. We will represent cell that is on the intersection of row x and column y by a pair of integers (x, y).

Valera wants to place exactly k tubes on his rectangle table. A tube is such sequence of table cells (x₁, y₁), (x₂, y₂), ..., (x_r, y_r), that:

• r ≥ 2;
• for any integer i (1 ≤ i ≤ r - 1) the following equation |x_i - x_i + 1| + |y_i - y_i + 1| = 1 holds;
• each table cell, which belongs to the tube, must occur exactly once in the sequence.

Valera thinks that the tubes are arranged in a fancy manner if the following conditions are fulfilled:

• no pair of tubes has common cells;
• each cell of the table belongs to some tube.

Help Valera to arrange k tubes on his rectangle table in a fancy manner.

The first line contains three space-separated integers n, m, k (2 ≤ n, m ≤ 300; 2 ≤ 2k ≤ n·m) — the number of rows, the number of columns and the number of tubes, correspondingly.

Print k lines. In the i-th line print the description of the i-th tube: first print integer r_i (the number of tube cells), then print 2r_i integers x_i1, y_i1, x_i2, y_i2, ..., x_iri, y_iri (the sequence of table cells).

If there are multiple solutions, you can print any of them. It is guaranteed that at least one solution exists.

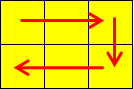
3 3 3

3 1 1 1 2 1 3
3 2 1 2 2 2 3
3 3 1 3 2 3 3

2 3 1

6 1 1 1 2 1 3 2 3 2 2 2 1

 Note

Picture for the first sample: 
 
  

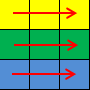
Picture for the second sample: