置换群求幂
TimeLimit:1000MS MemoryLimit:128MB
64-bit integer IO format:%lld
未提交 | 登录后收藏
Problem Description
置换群的定义如下:
设S={1,2,……n},S上的任何一个双射函数S->S构成了S上n个元素的置换,称为n元置换。
同通俗点说,就是设P1,P2为1到n的一个排列。
f为一个映射,且满足
f(p1(i))=p2(i) (其中p(i)代表 排列p上的第i个数字)
则称为f一个n元置换,f可以表示成如下形式
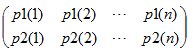
因为置换的表示具有列可交换性,所以同一个置换的表示方法并不唯一
比如以下几种表示都是等价的,表示的都是同一个置换
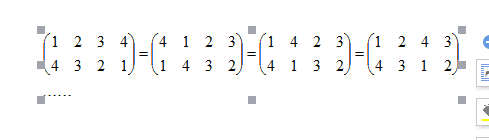
所以一般情况下,为表示方便取p1=1,2,3,4,5……n,即
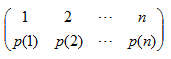
这称为n元置换的一般形式
n元置换的乘法定义如下
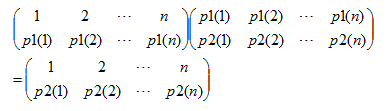
比如
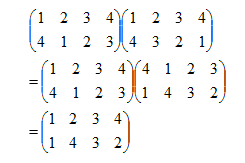
————————————————————————
问题:
现在给出p1和m求满足以下等式的p2
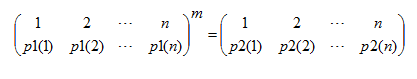
Input
多组测试数据
每组数据第一行是两个整数n m
接下来有n个数字代表p1
其中n<20
0<m<10^9
Output
对于每个案列输出一个1-n的排列代表p2,相邻数字间用空格隔开
SampleInput
12 2 2 3 6 8 10 7 1 9 4 12 11 5 12 9 9 1 11 6 4 3 2 5 7 10 12 8 8 2 6 4 7 8 2 3 5 1 16 3 14 9 3 6 16 13 8 10 4 11 2 15 7 5 1 12 14 18 6 4 8 1 2 5 3 14 12 13 11 10 7 9
SampleOutput
3 6 7 9 12 1 2 4 8 5 11 10 9 1 12 3 6 11 2 4 7 10 8 5 3 8 5 1 4 7 2 6 16 6 3 7 15 8 11 2 13 9 4 14 10 12 5 1 2 6 14 5 1 4 8 9 10 7 11 13 3 12
AC该题后可以添加标签
贴完标签可以获得20ACB。
并且可以获得本题所有提交代码查看权限。
点击标题可以显示标签。
如果你还没认真思考过这题,请不要查看标签
如果您已经通过了该题,请务为该题贴上标签
贴完标签可以获得20ACB。
并且可以获得本题所有提交代码查看权限。
点击标题可以显示标签。
如果你还没认真思考过这题,请不要查看标签
如果您已经通过了该题,请务为该题贴上标签