Inversions After Shuffle

You are given a permutation of integers from 1 to n. Exactly once you apply the following operation to this permutation: pick a random segment and shuffle its elements. Formally:

1. Pick a random segment (continuous subsequence) from l to r. All 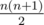segments are equiprobable.
2. Let k = r - l + 1, i.e. the length of the chosen segment. Pick a random permutation of integers from 1 to k, p₁, p₂, ..., p_k. All k! permutation are equiprobable.
3. This permutation is applied to elements of the chosen segment, i.e. permutation a₁, a₂, ..., a_l - 1, a_l, a_l + 1, ..., a_r - 1, a_r, a_r + 1, ..., a_n is transformed to a₁, a₂, ..., a_l - 1, a_{l - 1 + p1}, a_{l - 1 + p2}, ..., a_{l - 1 + pk - 1}, a_{l - 1 + pk}, a_r + 1, ..., a_n.

Inversion if a pair of elements (not necessary neighbouring) with the wrong relative order. In other words, the number of inversion is equal to the number of pairs (i, j) such that i < j and a_i > a_j. Find the expected number of inversions after we apply exactly one operation mentioned above.

The first line contains a single integer n (1 ≤ n ≤ 100 000) — the length of the permutation.

The second line contains n distinct integers from 1 to n — elements of the permutation.

Print one real value — the expected number of inversions. Your answer will be considered correct if its absolute or relative error does not exceed 10^- 9.

Namely: let's assume that your answer is a, and the answer of the jury is b. The checker program will consider your answer correct, if .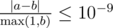

3
2 3 1

1.916666666666666666666666666667