Babaei and Birthday Cake

As you know, every birthday party has a cake! This time, Babaei is going to prepare the very special birthday party's cake.

Simple cake is a cylinder of some radius and height. The volume of the simple cake is equal to the volume of corresponding cylinder. Babaei has n simple cakes and he is going to make a special cake placing some cylinders on each other.

However, there are some additional culinary restrictions. The cakes are numbered in such a way that the cake number i can be placed only on the table or on some cake number j where j < i. Moreover, in order to impress friends Babaei will put the cake i on top of the cake j only if the volume of the cake i is strictly greater than the volume of the cake j.

Babaei wants to prepare a birthday cake that has a maximum possible total volume. Help him find this value.

The first line of the input contains a single integer n (1 ≤ n ≤ 100 000) — the number of simple cakes Babaei has.

Each of the following n lines contains two integers r_i and h_i (1 ≤ r_i, h_i ≤ 10 000), giving the radius and height of the i-th cake.

Print the maximum volume of the cake that Babaei can make. Your answer will be considered correct if its absolute or relative error does not exceed 10^- 6.

Namely: let's assume that your answer is a, and the answer of the jury is b. The checker program will consider your answer correct, if .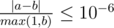

2
100 30
40 10

942477.796077000

4
1 1
9 7
1 4
10 7

3983.539484752

 Note

In first sample, the optimal way is to choose the cake number 1.
In second sample, the way to get the maximum volume is to use cakes with indices 1, 2 and 4.