Kadj Squares
In this problem, you are given a sequence S1, S2, ..., Sn of squares of different sizes. The sides of the squares are integer numbers. We locate the squares on the positive x-y quarter of the plane, such that their sides make 45 degrees with x and y axes, and one of their vertices are on y=0 line. Let bi be the x coordinates of the bottom vertex of Si. First, put S1 such that its left vertex lies on x=0. Then, put S1, (i > 1) at minimum bi such that
- bi > bi-1 and
- the interior of Si does not have intersection with the interior of S1...Si-1.
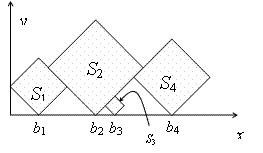
The goal is to find which squares are visible, either entirely or partially, when viewed from above. In the example above, the squares S1, S2, and S4 have this property. More formally, Si is visible from above if it contains a point p, such that no square other than Si intersect the vertical half-line drawn from p upwards.
The input consists of multiple test cases. The first line of each test case is n (1 ≤ n ≤ 50), the number of squares. The second line contains n integers between 1 to 30, where the ith number is the length of the sides of Si. The input is terminated by a line containing a zero number.
For each test case, output a single line containing the index of the visible squares in the input sequence, in ascending order, separated by blank characters.
4 3 5 1 4 3 2 1 2 0
1 2 4 1 3